Billyard
Time Limit: 3 Seconds Memory Limit: 65536 KB
Bill has invented a new game in the yard of his home called as Billyard. In this game, he has made a tall vertical board with some guns on its left or right vertical boarders as shown in the figure.
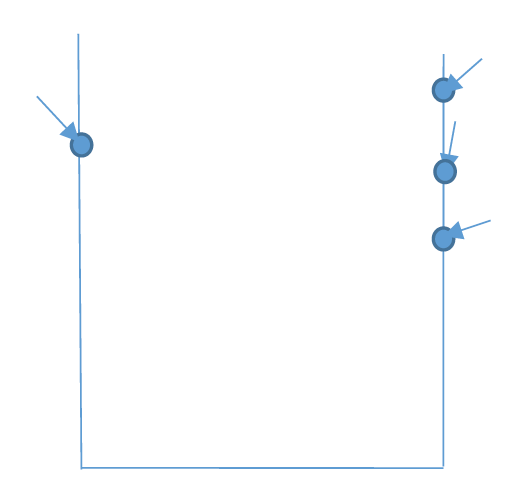
At the time 0, each gun shoots a ball toward the ground with a specified power and horizontal angle. Each ball moves with a constant speed along a straight path until reaches one of the borders (left, right or bottom). After such contact, the ball is reflected with opposite angle respect to the boarder. Due to that there is no upper boarder; these balls may be thrown out of the game board and may be lost. You should trap all of them in the board by putting a horizontal wood at top of them at a time t≥0. It is desired to minimize the distance of the wood from the ground. You can put this wood just once and changing its location is not easy. Hence, you can wait for the best opportunity.
Input
he number of test-cases is given as T<=100 in the first line. In following, each test-case is started by a line containing positive integers L, R and N, all less than 1,000. L and R are x-positions of left and right boarders, respectively. In followed N lines, positions of balls are described, one line per ball. In each line positive integers X0, Y0, X1 and Y1 as coordination of associated ball at time t=0 and t=1 have been given, respectively. It is clear that, X0 is equal to L or R. In addition, following conditions are true: L≤X1≤R and 0≤Y1<Y0≤109. No ball reaches the ground sooner than t=1. You can assume that due to have 3 dimensions, balls never contact to each other.
Output
For each test-case, print the best y-position of the wood with two digits after decimal point.
Sample Input
2 5 7 2 5 10 6 9 7 9 6 7 0 10 4 0 1000 0 800 0 900 0 650 0 900 0 800
Sample Output
3.67 516.67Submit
Source: 13th Iran Nationwide Internet Contest - Shiraz