Hexagonal connectivity

Time Limit: 5 Seconds    Memory Limit: 65536 KB

Having a hex world which some tile has a color of Red, Blue, Green or Gray and rest of them have no color (or white). We want to know what is the minimum number of colors that we have to walk to get from tile number A to tile number B. Note that we cannot walk over tiles which have no color (or white tiles).

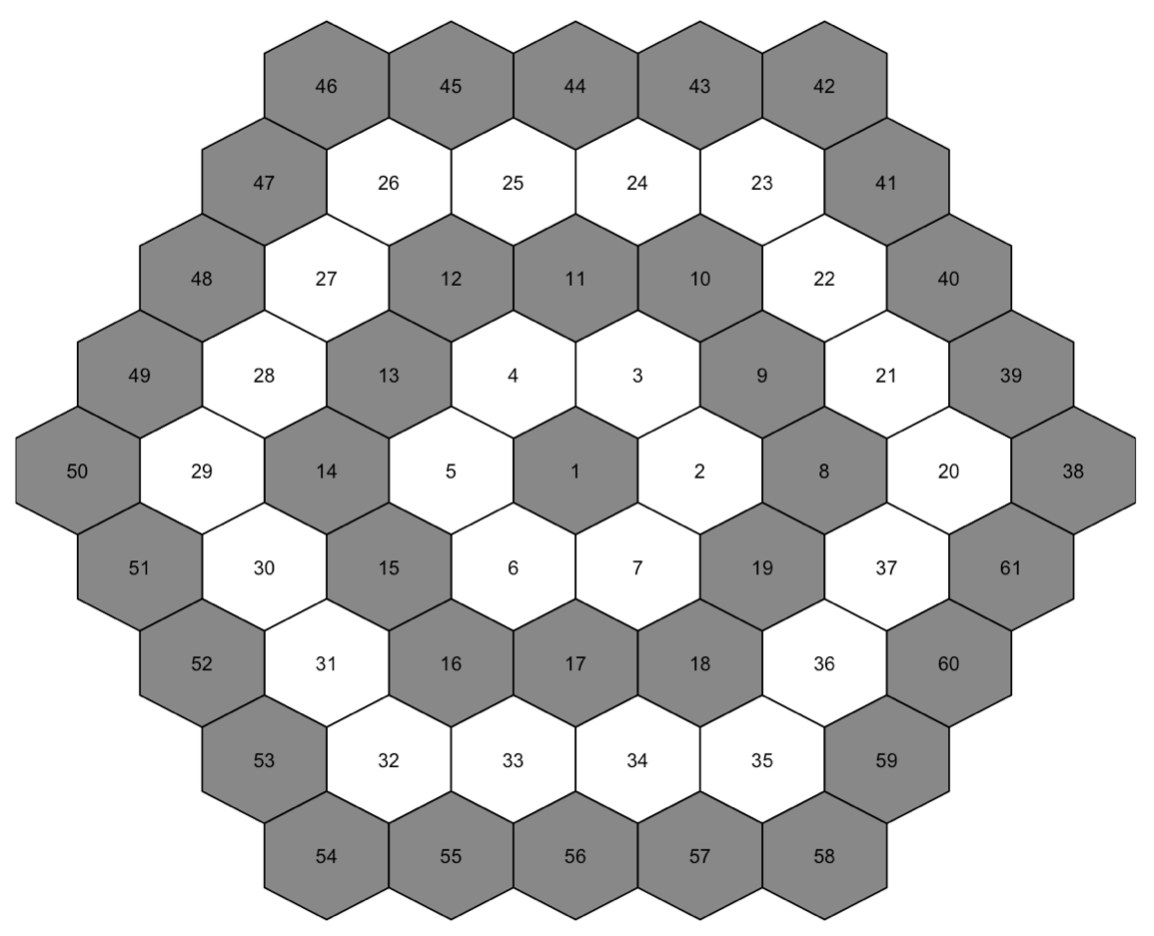
The indexing system is like above. 

Input

Input consists of several test cases, each test case is started with two integers, N and M. N representing the number of tiles with color and M the number of paired tiles which we want to know the minimum colors for getting from one to another.

Then there are N line, each having a tile number and a color (red, blue, green, gray), separated by “-“. And after that there are M lines each having 2 tile indexes (which both were noticed in the N lines) N would be less than 100000.

Output

For each 2 tiles, input 0 if there is no path and if there is a path, output the minimum number of colors needed to get through. 

Sample Input

5 3
1-gray
2-gray
8-gray
37-green
60-gray
1 60
1 37
7 8

Sample Output

2
2
0

Submit

Source: 13th Iran Nationwide Internet Contest - SBU