History-Cleanable DFA

Time Limit: 3 Seconds    Memory Limit: 65536 KB

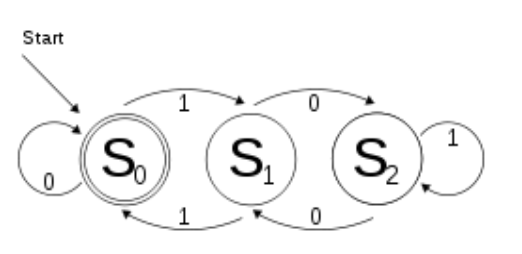
You have possibly heard of DFAs. In theory of computation, a deterministic finite automaton (DFA) is a finite state machine that accepts/rejects finite input strings. The figure on the right illustrates a DFA using a state diagram. In the automaton, there are three states: S₀, S₁, and S₂ (denoted graphically by circles). The automaton takes a finite sequence of 0s and 1s as input. For each state, there is a transition arrow leading out to a next state for both 0 and 1. Upon reading a symbol, a DFA jumps from a state to another by following the transition arrow. For example, if the automaton is currently in state S₀ and current input symbol is 1 then it jumps to state S₁. This is formally written as δ(S₀,1)=S₁. Inductively, we can generalize this notation to have propositions like δ(S₀,10)=S₂ and δ(S₁,011010)=S₀. A DFA has a start state (denoted graphically by an arrow coming in from nowhere) where computations begin with, and a set of accept states (denoted graphically by a double circle) which help define when a computation is successful. So, an input string w is accepted by a DFA with starting state q₀ if and only if δ(q₀,w) is an accepting state of that DFA. The state S₀ in the DFA depicted above is both the start state and an accept state. In fact, this DFA accepts only binary numbers that are multiples of 3 (including the empty string).

Given a DFA D with states S₀,S₁,…,S_n-1, a string w is called history-cleaner for D if for all i,j∈{0,…,n-1}: δ(S_i,w)=δ(S_j,w). In other words, no matter which state the starting state is, the string w brings the DFA to a common final state. A DFA D is called history-cleanable if a history-cleaner string exists for D. Given a DFA whose input is a sequence of 0s and 1s, your job is to find out whether it is history-cleanable or not.

Input

The first line of the input contains the single integer t, the number of test cases (1≤t≤500). Each test case starts with a line containing a single integer n, the number of states in a DFA with states S₀,S₁,…,S_n-1 (2≤n≤500). The second line of each test case consists of n space-separated integers a₀,a₁,…,a_n-1 and finally, the third line of each test case has n space-separated integers b₀,b₁,…,b_n-1 (0≤a_i,b_i<n) which means δ(S_i,0)=S_ai and δ(S_i,1)=S_bi (for 0≤i<n).

Output

For each test case, print one line containing the answer for the given DFA. If it is history-cleanable, print “YES”, otherwise print “NO” (omit the quotes).

Sample Input

2 
4 
1 2 3 0 
3 0 1 0 
4 
1 2 3 0 
2 2 1 2

Sample Output

NO 
YES

Submit

Source: 13th Iran Nationwide Internet Contest - Final