F :: Special Camera Linearity

Time Limit: 15 Seconds    Memory Limit: 65536 KB

Having 3 cameras, we call these cameras Linear, if they fulfill the below condition.

Imagine C1, C2 and C3 are the 3 cameras, each one having their angle of view. We call the Intersection of the Left view line of C1 and the same line of C2, L12, and Right view line of C1 and the same line of C2, R12   and like that we create 6 intersections, L12, L13, L23, R12, R13 and R23 . As it can be seen, L12R12 is the only line of view that is common in the view of C1 and C2. Lines of views are L12R12, L13R13, L23R23. If these three lines have the same point of intersection, we call these 3 cameras special Linear. 

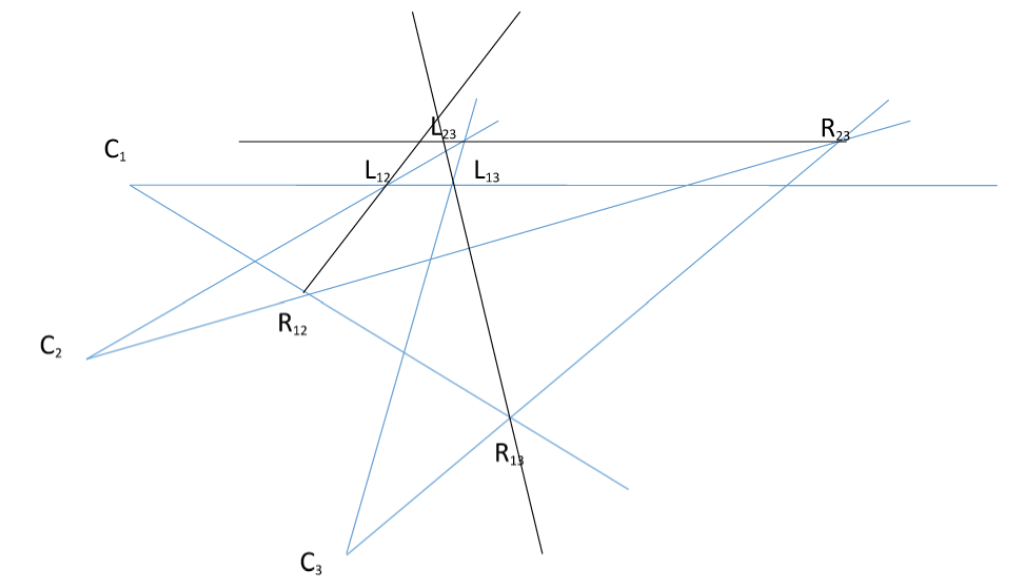
Knowing this definition, we have N cameras, all with a degree view of 30 degrees and random rotation pattern which ensures all possible cross overs between these cameras, your job is to calculate the number of three triplet cameras that are linear.

Input

Input consists of several test cases. Each test case starts an Integer N, the number of cameras on the field (which is less than 10000). This integer is followed by N lines, each having 2 integers, the coordinates of cameras (x, y) in which are less than 10000.

Output

For each Input, output the number of triplets that are by the above definition, Linear, in at least one possible cross over. 

Sample Input

1
4
0 0
1 1
0 1
1 0
6
0 0
0 1
0 2
0 3
1 0
1 1

Sample Output

0
4

Submit

Source: 13th Iran Nationwide Internet Contest - SBU