I :: Intersections

Time Limit: 10 Seconds    Memory Limit: 32768 KB

There are N red points numbered from 1 to N, and also N blue points numbered from 1 to N  around a circle. We want to connect each red points to its corresponding number in blue points and then counting number of all intersections which occur. Given the order of blue and red points around the circle, your task is to count number of all intersections after connecting points in a mentioned way.

You can assume that no 3-pair of points intersect at the same position.(i.e you should  count all pairs of intersecting pairs separately)

 

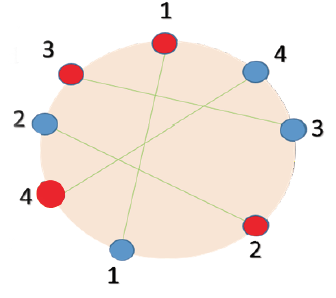
Input

input contains several test cases. Each test case is composed by three lines. The first line contains an integer N, indicating number of red and blue points 1<N<100000. The second line contains a string S, consisting of ‘R’ and ‘B’ characters that are clockwise order of blue and red points. The third line contains 2*N integers P₀, P₁, ..., P_2N separated by spaces. Pi is the number of each corresponding character in second line. so the i-th point around the circle (from wherever you start, in clockwise order) has the number P_i and color S_i.

You can assume that input is valid, i.e. there are exactly N of ‘R’ and N of ‘B’ characters in S. Also each number P_i comes exactly twice and color of same numbers are different. 

The input ends with a single zero.

 

Output

For each test case in the input, print the number of intersections as mentioned above.

 

Sample Input

4
RBBRBRBR
1 4 3 2 1 4 2 3
3
RRBBRB
1 2 2 1 3 3
0

Sample Output

5
0

Submit

Source: 12th Iran Nationwide Internet Contest III