Sequence
Time Limit: 1 Second Memory Limit: 65536 KB
We inductively label the nodes of a rooted binary tree with an infinite number of nodes as follows:
- The root is labeled by 1/1,
-
If the label of a node is p/q, then
- The label of its left child is p/(p+q), and
- The label of its right child is (p+q)/q.
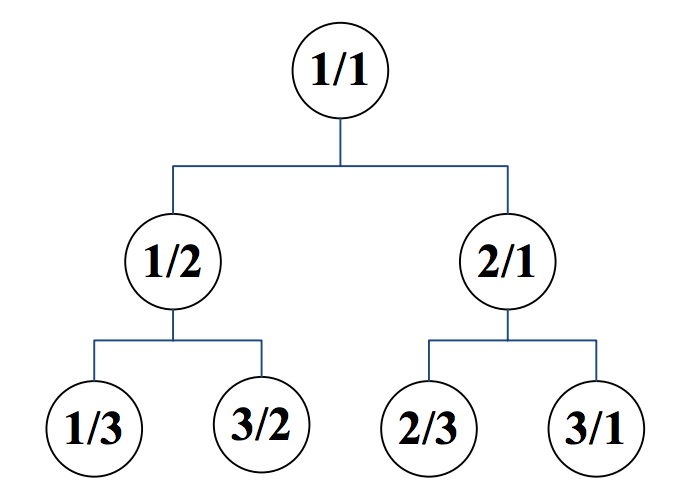
By having this tree in our hand, we define a rational sequence a1, a2, a3, … by a breadth first traversal of the tree in such a way that nodes in the same level are visited from left to right. Therefore, we have a1=1/1, a2=1/2, a3=2/1, a4=1/3, a5=3/2, …
You are to write a program that gets values p and q and computes an integer n for which an=p/q.
Input
The first line of the input includes the number of test cases, 1≤t≤1000. Each test case consists of one line. This line contains p, followed by / and then q without any space between them.
Output
For each test case, output in one line an integer n for which an=p/q. It is guaranteed that in all test cases n fits in a 32-bit integer.
Sample Input
4 1/1 1/3 5/2 2178309/1346269
Sample Output
1 4 11 1431655765Submit
Source: 13th Iran Nationwide Internet Contest - Final