F :: Tape the Art

Time Limit: 2 Seconds    Memory Limit: 65536 KB
Special Judge

Bahman is a perfect artist who produced some paintings in the shape of a chessboard. His paintings are all the same but different in width and height. He always chooses a piece of paper sized Mcm × Ncm. He divides the paper with imaginary lines to create M × N little 1cm × 1cm squares, and then he paints the squares with two colors (black and white) like a chessboard. In order to put his work in a gallery, they have to tape them into the wall. They will use a very low-width tape (just like a direct line) and will tape that from the top-right corner of the artwork to its bottom-left. As the tape should be colored exactly the same as the color of the square underneath, we want to compute the total length of the black part of the tape.

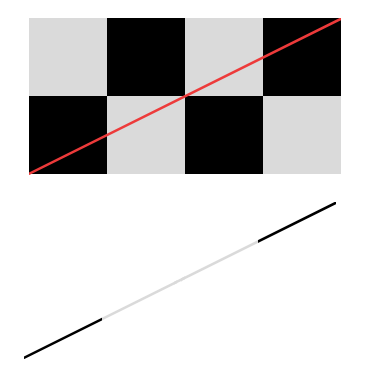
Assume the bottom-left square is always black.

Input

The input contains several test cases.
In the first line of input comes T (0 < T < 10000), the number of test cases.
Each case is a line containing two integers M, N(1 ≤ M,N ≤ 2³¹ - 1).

Output

For each case, output a single line containing the length of the line colored black, rounded up to 3 digits after the decimal point.

Sample Input

2
2 4
3 6

Sample Output

2.236
3.354

Submit

Source: 12th Iran Nationwide Internet Contest - Final